선형 회귀(Linear Regression)
1. 선형회귀
1.1 회귀(Regression)
Training Data를 이용하여 데이터의 특성과 상관관계 등을 파악하고, 그 결과를 바탕으로 Training Data에 없는 미지의 데이터(Test Data)가 주어졌을 경우에, 그 결과를 연속적인(숫자) 값으로 예측하는 것 ==> 대부분 머신러닝 문제는 지도학습에 해당됨
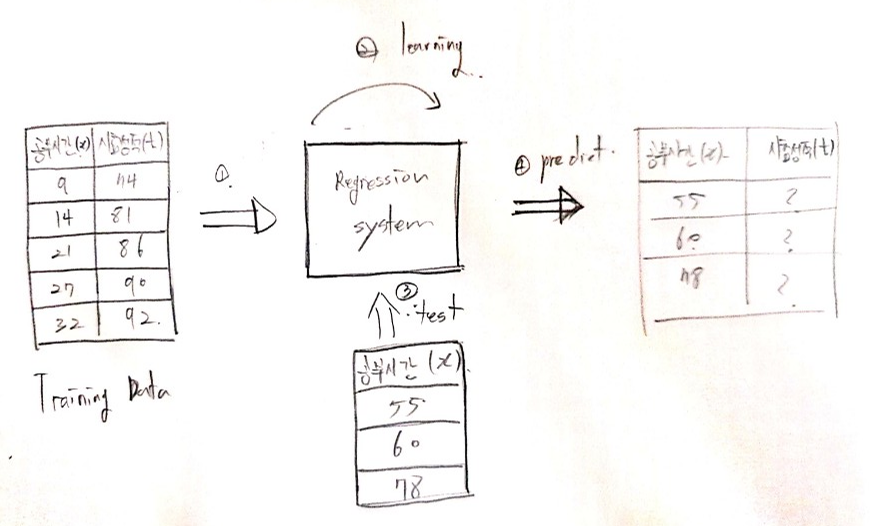
머신러닝시스템에서의 학습(learning)의 개념
Training Data를 분석하여 다양한 y = Wx + b 중에서 Training Data의 특성을 가장 잘표현할수 있는 가중치 W(기울기), 바이어스(b)를 찾는것이 학습(learning)의 개념임
1.2 선형 회귀란 ??
공부 시간을 늘리면 시험 성적이 잘나온다. 집의 평수가 클수록, 가격은 비싼경향이 있다. 이런 사례를 수학적으로 생각해보면 어떤 요인에 의해 특정 요인의 수치가 영향을 받음을 알수있다.
수학적으로 표현해본다면 변수 x에 의해 종속적으로 변하는 변수 y가 있는데, 변화정도가 선형 상관관계를 갖는긱법이다.
1.2.1 단순 선형 회귀 분석 (한 개의 변수에 의해)
- 독립변수 x에 의해 종속변수 y가 변하는 수식

1.2.2 다중 선형 회귀 분석(둘 이상의 변수에 의해)
- 독립변수 x1, x2 ...., xn에 의해 y가 변하는 수식

2. 가설(Hypothesis) 세우기
단순 선형 회귀를 통해 가설을 세워보자!
Training Data
| 공부시간(x) | 시험성적(y) |
|---|---|
| 2 | 25 |
| 3 | 50 |
| 4 | 42 |
| 5 | 61 |

Training Data의 4개의 데이터로부터 x와 y의 관계과 가장 유사한 H(x) = Wx + b을 찾아야하는데, 머신러닝에선 이러한 식을 가설이라고 한다.
파란색 점(훈련데이터)와 가장 유사한 직선을 찾아내기 위해 적절한 W와 b를 찾는것이 핵심!!
3. 비용함수(Cost function) ==> 평균제곱오차(MSE)
앞서 W와 b를 구하는것이 핵심이라고 했는데, 그렇다면 W와 b는 어떻게 구할까 ??
바로 비용함수를 통해 구하자!!
비용함수란?
- 실제값과 예측값에 대한 오차를 의미한다.
- 목적함수(Objective function) 또는 손실 함수(loss function) 라고도 한다
비용함수는 주로 평균 제곱 오차(Mean Squared Error, MSE)로 사용된다.

- y절편을 활용하여 점의 위치 y, 임의의 직선 H(x)의 오차의 제곱을 구한뒤(오차 = y-H(x))
- 모든 데이터의 부호를 없애기 위해 제곱을 한다
- 평균오차를 구해주기위해 데이터의 갯수 n으로 나눠준다
4. 옵티마이저: 경사하강법(gradient decent algorithm)
- 선형회귀를 포함한 수많은 머신 러닝, 딥러닝의 학습은 결국 비용 함수를 최소화하는 W, b를 찾기위한 작업을 수행하고, W와 b를 찾아내는 과정을 머신 러닝에서 학습(training)이라고 부른다.
- 경사하강법은 그 학습(training)중에 가장 기본적인 알고리즘이다.
- cost(W, b)의 값이 최소가 되는 W와 b를 구하여 손실이 최소가되어 Training Data의 x와 y의 관계과 가장 유사한
H(x) = Wx + b을 찾을수있다. - 이를 위해 cost - W 의 관계는 2차함수관계를 활용하여, 접선의 기울기가 최소인 W인 점을 찾는다.

[1] 임의의 가중치 W를 선택 ==> 해당 위치의 미분값이 0이 아닌경우
[2] 그 W에서의 E - W 2차 그래프의 기울기 절댓값이 작아지는 방향으로 W가 감소 or 증가
기울기의 절댓값이 작아지는 방향의 의미: 기울기가 0인 수평한 직선을 찾아라!!!!- 임의의 W에서의 기술기가 양수값
(/)이면 가중치 W값을 왼쪽으로 이동(W값 감소), 음수값이면(\)가중치 W값을 오른쪽으로 이동(W값 증가)- 이때 W의 값을 증가 or 감소를위해 학습률(learning rate)을 W에 곱하면서 증가 or 감소를 한다.
[3] 감소하다가 더이상 감소하지 않는 그 시점이 바로 cost(W, b)가 최소값임을 알수 있다.
결론
머신 러닝의 학습은 결국 비용함수를 최소화를 시키는 매개변수 W와 b를 찾는과정!!!!
5. Linear Regression 코드 구현
1) 직접 알고리즘을 구현
입력데이터 (x_data) 1개일때, Regression를 활용 하여 testdata의 예측결과값을 구해보자
import numpy as np
# [1] 1개의 훈련데이터를 갖는 단순 선형회귀
# 입력 : 공부하는 시간
x_data = np.array([1,2,3,4,5,6,7,8,9]).reshape(9,1)
# 정답 : 성적
t_data = np.array([11,22,33,44,53,66,77,87,95]).reshape(9,1)
# [2] 임의의 가중치와 bias를 랜덤으로 정의
W = np.random.rand(1,1)
b = np.random.rand(1)
# MSE를 활용한 손실 함수(비용함수)
def loss_func(x, t):
y = np.dot(x,W) + b
return ( np.sum( (t - y)**2 ) ) / ( len(x) )
# 미분을 위한 함수
def numerical_derivative(f, x):
delta_x = 1e-4 # 0.0001
grad = np.zeros_like(x)
it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
while not it.finished:
idx = it.multi_index
tmp_val = x[idx]
x[idx] = float(tmp_val) + delta_x
fx1 = f(x) # f(x+delta_x)
x[idx] = tmp_val - delta_x
fx2 = f(x) # f(x-delta_x)
grad[idx] = (fx1 - fx2) / (2*delta_x)
x[idx] = tmp_val
it.iternext()
return grad
# 손실함수 값 계산 함수
# 입력변수 x, t : numpy type
def error_val(x, t):
y = np.dot(x,W) + b
return ( np.sum( (t - y)**2 ) ) / ( len(x) ) # 오차값 : 실제값과 훈련결과값의 차이
# 학습을 마친 후, 임의의 데이터에 대해 미래 값 예측 함수
# 입력변수 x : numpy type
def predict(x):
y = np.dot(x,W) + b
return y
learning_rate = 1e-2 # 발산하는 경우, 1e-3 ~ 1e-6 등으로 바꾸어서 실행
f = lambda x : loss_func(x_data,t_data)
print("Initial error value = ", error_val(x_data, t_data), "Initial W = ", W, "\n", ", b = ", b )
# 8000번의 훈련을 진행
for step in range(8001):
# [3] 가중치와 bias의 업데이트 위해 f에 대한 W와 b에 대해 편미분을 한다
W -= learning_rate * numerical_derivative(f, W)
b -= learning_rate * numerical_derivative(f, b)
# [4] 400번의 훈련마다 손실함수를 계산한다.
if (step % 400 == 0):
print("step = ", step, "error value = ", error_val(x_data, t_data), "W = ", W, ", b = ",b )
print(predict(25))Initial error value = 3238.067135412484 Initial W = [[0.66605681]], b = [0.21615434]
step = 0 error value = 422.5327084122304 W = [[7.06927206]] , b = [0.58934849]
step = 400 error value = 1.059876770588233 W = [[10.6834985]] , b = [0.80451639]
step = 800 error value = 1.0598765512297794 W = [[10.68336435]] , b = [0.80536039]
step = 1200 error value = 1.059876543492748 W = [[10.68333916]] , b = [0.8055189]
step = 1600 error value = 1.059876543219859 W = [[10.68333443]] , b = [0.80554867]
step = 2000 error value = 1.0598765432102293 W = [[10.68333354]] , b = [0.80555426]
step = 2400 error value = 1.0598765432098862 W = [[10.68333337]] , b = [0.80555531]
step = 2800 error value = 1.059876543209873 W = [[10.68333334]] , b = [0.80555551]
step = 3200 error value = 1.059876543209871 W = [[10.68333333]] , b = [0.80555555]
step = 3600 error value = 1.0598765432098691 W = [[10.68333333]] , b = [0.80555555]
step = 4000 error value = 1.059876543209878 W = [[10.68333333]] , b = [0.80555556]
step = 4400 error value = 1.0598765432098765 W = [[10.68333333]] , b = [0.80555556]
step = 4800 error value = 1.05987654320988 W = [[10.68333333]] , b = [0.80555556]
step = 5200 error value = 1.0598765432098818 W = [[10.68333333]] , b = [0.80555556]
step = 5600 error value = 1.059876543209874 W = [[10.68333333]] , b = [0.80555556]
step = 6000 error value = 1.059876543209869 W = [[10.68333333]] , b = [0.80555556]
step = 6400 error value = 1.059876543209875 W = [[10.68333333]] , b = [0.80555556]
step = 6800 error value = 1.0598765432098811 W = [[10.68333333]] , b = [0.80555556]
step = 7200 error value = 1.0598765432098765 W = [[10.68333333]] , b = [0.80555556]
step = 7600 error value = 1.0598765432098818 W = [[10.68333333]] , b = [0.80555556]
step = 8000 error value = 1.059876543209881 W = [[10.68333333]] , b = [0.80555556]
[[267.88888889]]2) 케라스로 선형회귀를 구현
from keras.models import Sequential # 케라스의 Sequential()을 임포트
from keras.layers import Dense # 케라스의 Dense()를 임포트
from keras import optimizers # 케라스의 옵티마이저를 임포트
import numpy as np # Numpy를 임포트
# 1. Training Data
X=np.array([1,2,3,4,5,6,7,8,9]) # 공부하는 시간
y=np.array([11,22,33,44,53,66,77,87,95]) # 각 공부하는 시간에 맵핑되는 성적
# 2. 모델생성
# Sequential()으로 모델을 만들고 add로 필요한 사항들을 추가
# Dense(출력의 차원, input_dim=입력의차원, activation=어떤함수를사용할건가?), 선형회귀일경우: 'linear'
model=Sequential()
model.add(Dense(1, input_dim=1, activation='linear'))
# 학습률(learning rate, lr): 0.01
sgd=optimizers.SGD(lr=0.01)
# sgd는 경사 하강법을 의미
# 손실 함수(Loss function)은 평균제곱오차 mse를 사용합니다.
model.compile(optimizer=sgd ,loss='mse',metrics=['mse'])
# 주어진 X와 y데이터에 대해서 오차를 최소화하는 작업을 300번 시도합니다.
model.fit(X,y, batch_size=1, epochs=300, shuffle=False)
import matplotlib.pyplot as plt
plt.plot(X, model.predict(X), 'b', X,y, 'k.')
print(model.predict([25]))'Data Science > 머신러닝' 카테고리의 다른 글
| 딥러닝 기초 나만의 정리 2 (0) | 2020.09.16 |
|---|---|
| 딥러닝 기초 나만의 정리 (0) | 2020.07.08 |
| LSTM으로 IMDB 리뷰 감성 분류하기 (0) | 2020.07.02 |
| Logistic Regression(Classification) 나만의 정리 (0) | 2020.06.28 |
| 지도학습과 비지도학습 나만의 정리 (0) | 2020.06.26 |
| 수치미분 나만의 정리 (0) | 2020.06.26 |
| matplotlib 라이브러리 (0) | 2020.06.25 |
| numpy 라이브러리 (1) | 2020.06.24 |