728x90
자료구조 힙(heap)이란 ?
힙은 완전 이진트리의 일종으로 우선순위 큐를 위해 만들어진 자료구조이다.
여러개의 값중에서 최대값이나 최소값을 빠르게 찾아내는 구조다.
힙 트리의 경우에는 중복된 값을 허용한다(이진 탐색 트리에서는 중복된 값을 허용하지 않는다.)
힙(heap)의 종류
힙의 종류는 최대힙과 최소힙이있다.
최대힙(max heap)
부모의 노드값이 자식 노드의 값보다 큰 완전 이진 트리
최소힙(min heap)
부모의 노드값이 자식 노드의 값보다 작은 완전이진트리
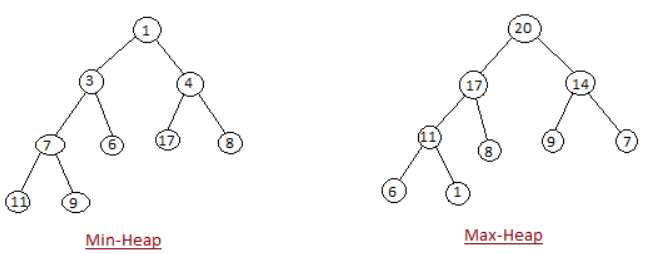
힙(heap)의 성질
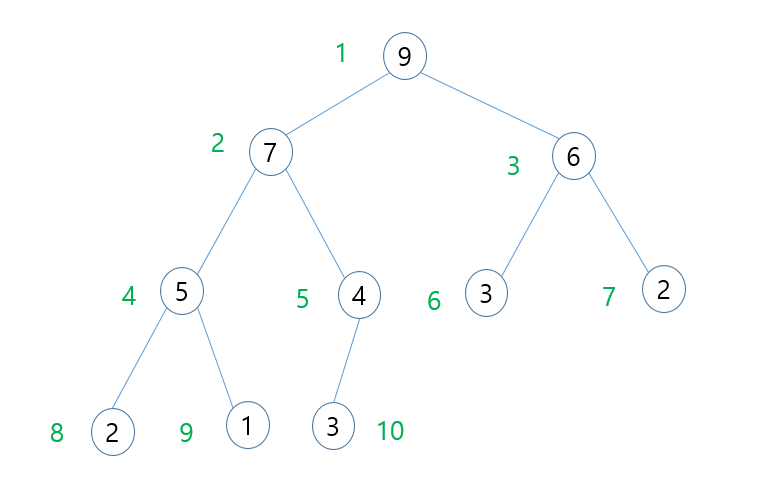
- 힙에서 부모 노드와 자식 노드의 관계
왼쪽 자식의 인덱스 = (부모 인덱스) x 2
오른 자식의 인덱스 = (부모 인덱스) x 2 + 1
부모의 인덱스 = (자식 인덱스) / 2
예시)
2 (숫자 7의 인덱스) = 1 (부모의 인덱스) x 2
3 (숫자 6의 인덱스) = 1 (부모의 인덱스) x 2 + 1
1 (부모 1의 인덱스) = 2 (왼쪽자식 인덱스) / 2
힙(heap)의 삽입
힙구조에 새로운 요소가 들어오는경우, 우선 마지막 노드 뒤에 삽입을 하고 그다음 힙의 성질에 맞게 위치를 이동 시킨다.
새로운 원소 8를 힙구조에 삽입한다면,
- 마지막노드에 8을 삽입시킨뒤 힙의 성질에 따라 부모노드인 4와 서로 교환
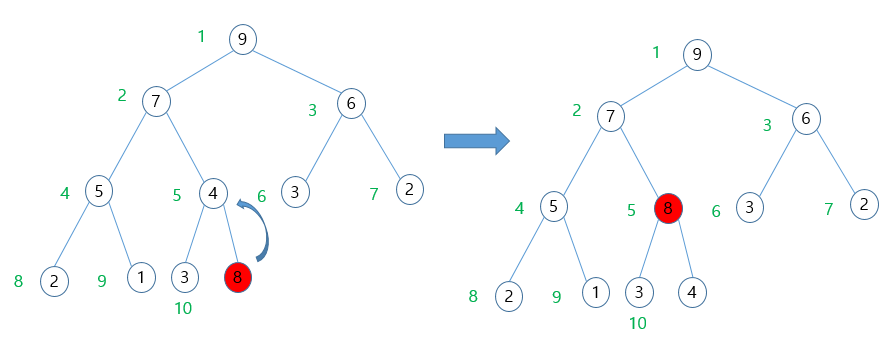
- 새로 위치한 노드에서 힙의 성질에 따라 부모노드 7과 서로 교환
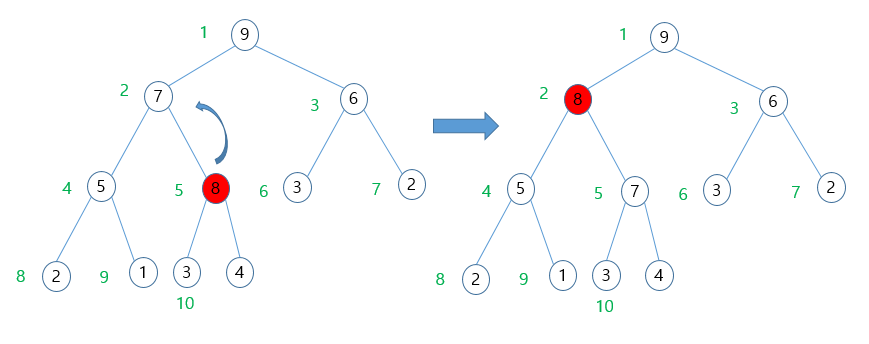
- 새로 위치한 노드에서 힙의 성질에 따라 부모노드 9와 교환하지 않는다.
python 코드
class BinHeap:
def __init__(self):
self.heapList = [0]
self.currentSize = 0
# 삽입하기 : 배열의 마지막에 삽입 (완전 이진트리의 맨 마지막에 넣는다.)
# 힙구조를 만들어줌
def insert(self,k): #self는 자기자신
self.heapList.append(k)
self.currentSize += 1
self.percUp(self.currentSize) # 새롭게 추가위치가 어디서 만들어지는데 알기위해
# 현재노드가 부모노드보다 작으면 자리변경 -> root까지 반복
def percUp(self,i):
# 나와 부모를 비교하는것
while i//2 > 0:
if self.heapList[i] < self.heapList[i//2]:
self.heapList[i], self.heapList[i // 2]= self.heapList[i//2],self.heapList[i]
i = i // 2
def printHeap(self):
print(self.heapList)
# 삭제
def delMin(self):
retval = self.heapList[1]
self.heapList[1] = self.heapList[self.currentSize]
self.currentSize -=1
self.heapList.pop()
self.percDown(1)
return retval
# 자식들중 최소값의 위치찾기
def minChild(self,i):
# 자식중 한개밖에 없으면
if i*2 +1 > self.currentSize:
return i*2 # 왼쪽자식 리턴
else:
# 왼쪽자식 < 오른쪽 자식이면
if self.heapList[i*2] < self.heapList[i*2+1]:
return i*2 # 더 최소인 작은 왼쪽자식을 리턴
else:
return i*2+1
def percDown(self,i):
while i+2 <=self.currentSize:
mc = self.minChild(i)
if self.heapList[i] < self.heapList[mc]:
self.heapList[i], self.heapList[mc] = self.heapList[mc],self.heapList[i]
i = mc
hp = BinHeap()
arr = [34,27,3,50,40]
for n in arr:
hp.insert(n)
hp.printHeap()
hp.delMin()
>>>
[0, 34]
[0, 27, 34]
[0, 3, 34, 27]
[0, 3, 34, 27, 50]
[0, 3, 34, 27, 50, 40]heapq를 활용한 코드
heapq의 경우 기본값이 최소힙구조로 되어있다.
만약 최대 힙으로 하려면 모든 원소들의 부호를 바꿔서 사용하면 된다.
import heapq
test = [1,3,2,6,8,0,6]
heapq.heapify(test)
# heapify : 기존의 리스트를 heap정렬로 만들어준다.
>>> test
[0, 3, 1, 6, 8, 2, 6]# heapq : push의 순서와 상관없이 Min - priority - queue 구조를 갖는다.
heapq.heappush(test, 3)
heapq.heappush(test, 5)
heapq.heappush(test, 1)
heapq.heappush(test, -3)
>>> test
[-3, 0, 1, 3, 1, 2, 6, 6, 5, 8, 3]
>>> heapq.heappop(test) # 가장 최소값(root)인 -3을 pop한다
-3728x90
'Computer Science > 자료구조' 카테고리의 다른 글
| Prim 알고리즘 - 최소 신장 트리(MST) (0) | 2020.11.07 |
|---|---|
| 퀵정렬(Quick Sort) (0) | 2020.11.03 |
| 병합정렬(Merge Sort) (0) | 2020.10.13 |
| 최소신장트리(MST) 나만의 정리 (0) | 2020.09.03 |
| Trie 나만의정리 (0) | 2020.08.23 |
| 그래프 나만의 정리 (0) | 2020.06.29 |
| 백트래킹(Backtracking) 나만의 정리 (0) | 2020.06.29 |
| 분할정복 (Devide and Conque)과 이진검색 (0) | 2020.06.29 |