728x90
Prim 알고리즘 - 최소 신장 트리(Minimum Spanning Tree)
최소 신장 트리(mst)란 ?
그래프에 있는 모든 정점들을 가장 적은 가중치의 합으로 연결하는것을 말한다.
MST의 특징
N개의 정점과 N-1개의 간선으로 이루어진 무방향 그래프
사이클을 형성하면 안된다.
대표적인 알고리즘으로 Prim 알고리즘, Kruskal 알고리즘, dijkstra알고리즘이 있다
MST는 도로건설이나 통신 등 거리나 비용을 최소로 요구하는곳에 사용됨
Prim 알고리즘
하나의 정점에서 연결된 간선들 중에 하나씩 선택면서 MST를 만들어가는 방식
- 시작 정점을 기준으로 하여 인접하는 정점들 중의 최소비용의 간선이 존재하는 정점을 선택
- N-1개의 간선을 가질때 까지 반복
과정
- 시작정점인 0번에서 가중치가 가장 작은 2번으로 이동
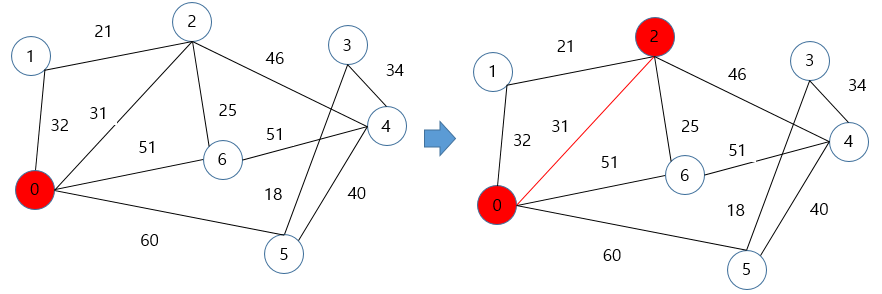
- 2번에서 가중치가 가장 작은 1번으로 이동하고, 1번에서 가중치를 갱신할 곳이 없기 때문에 2번의 다음 가중치 최소인 6번으로 이동
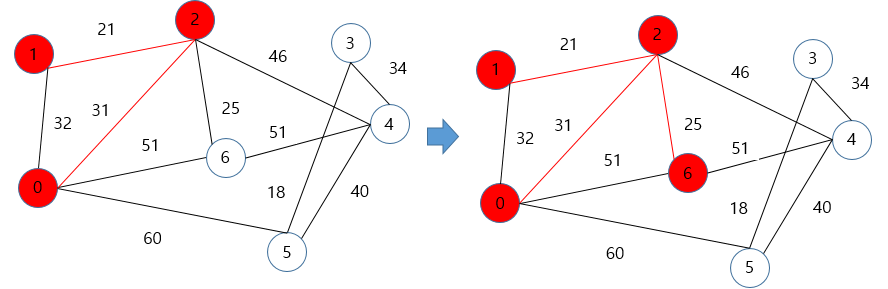
- 6번에서 가중치가 가장 작은 4번으로 이동한뒤, 4번에서 가중치가 가장 작은 3번으로 이동
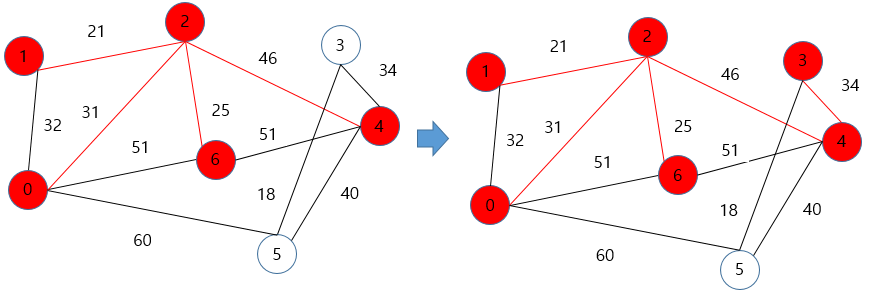
- 3번에서 가장 가중치가 작은 5번으로 이동
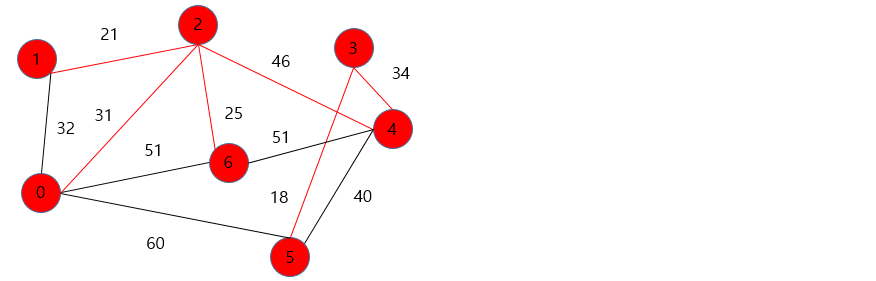
정점의 갯수는 총 7개고 간선은 11개지만 정점의 갯수 - 1 개인 6개의 간선을 돌면서 0번에서 시작한 최소 가중치의 합을 찾을수 있다.
python 코드
#인접행렬로 푼 문제
V, E = map(int,input().split()) # V: 정점
adj = [[0]*V for _ in range(E)]
for i in range(E):
s,e,c = map(int,input().split())
adj[s][e] = c
adj[e][s] = c
INF = float('inf') # 무한
key = [INF]*V # 각각의 노드 사이에서 최소 가중치 값이 있음
p = [-1]*V # 각각 객체에는 before 노드번호 있음
mst = [False] * V # 시작점이 다른 정점으로 이동을 했냐?? 의 유무
key[0] = 0
cnt = 0
result = 0 # 모든 가중치의 합
while cnt < V:
min = INF
u = -1
############################################################
# 인접 정점중 가중치값이 있는 key 배열에서 가장 작은 min값을 찾은뒤
# 해당 노드번호로 이동을 위한 u를 정의
############################################################
for i in range(V):
if not mst[i] and key[i] < min:
min = key[i]
u = i
############################################################
# 이동한 정점의 방문표시를 위한 true를 하고 result에 가중치를 더해준다
############################################################
mst[u] = True # 이동한 정점인 u가 방문했음을 표시
result += min
cnt += 1
############################################################
# 이동한 정점에서의 인접정점의 가중치(key)를 모두 저장시키고,
# 기존의 저장되있던 가중치보다 작을경우에도 다시 갱신을 한다,
# adj[u][w] > 0 : 인접행렬이 있고
# not mst[w] : 방문를 하지 않고
# key[w] > adj[u][w] : 기존의 저장된 가중치보다 작을경우에만
# 해당 인접 정점에 가중치를 저장하고 현재 위치 표시(p)를 한다.
# 주의!! 이동을 한것은 아니다!! 임시로 저장해둔것!!
############################################################
for w in range(V):
if adj[u][w] > 0 and not mst[w] and key[w] > adj[u][w]:
key[w] = adj[u][w]
p[w] = u
print(key) # 노드간의 가중치
print(p) # p배열의 각각의 현재 위치 index에 있는 숫자가 현재위치 이전의 노드번호
print(mst) # 방문배열
print(result) # 최단거리를의 가중치의 합
'''
7 11
0 5 60
0 1 32
0 2 31
0 6 51
1 2 21
2 4 46
2 6 25
3 4 34
3 5 18
4 5 40
4 6 51
'''Prim 알고리즘의 시간 복잡도
첫번째 반복문이 총 정점인 n번을 반복하고, 각각의 정점마다 n번을 반복하므로 시간복잡도는 O(n ^ 2)이 된다.
728x90
'Computer Science > 자료구조' 카테고리의 다른 글
| [자료구조] 힙(heap) 나만의정리 (0) | 2020.11.04 |
|---|---|
| 퀵정렬(Quick Sort) (0) | 2020.11.03 |
| 병합정렬(Merge Sort) (0) | 2020.10.13 |
| 최소신장트리(MST) 나만의 정리 (0) | 2020.09.03 |
| Trie 나만의정리 (0) | 2020.08.23 |
| 그래프 나만의 정리 (0) | 2020.06.29 |
| 백트래킹(Backtracking) 나만의 정리 (0) | 2020.06.29 |
| 분할정복 (Devide and Conque)과 이진검색 (0) | 2020.06.29 |