3장 신경망 시작하기2
3.5 뉴스기사 분류: 다중분류문제
이전 이중분류문제의 경우 2개의 클래스(긍정, 부정)를 분류하는 문제지만, 이번 문제는 46개의 클래로 분류하는 다중분류의 예입니다.
3.5.1 로이터 데이터셋
로이터 데이터셋은 46개의 토픽이 있으며, 각 토픽의 훈련세트는 최소한 10개의 샘플을 가지고 있습니다.
# 로이터 데이터셋 로드하기
from keras.datasets import reuters
(train_data, train_labels), (test_data, test_labels) = reuters.load_data(num_words=10000)
# 로이터 데이터셋을 텍스트로 디코딩하기
word_index = reuters.get_word_index()
reverse_word_index = dict([(value, key) for (key, value) in word_index.items()])
# 0, 1, 2는 '패딩', '문서 시작', '사전에 없음'을 위한 인덱스이므로 3을 뺍니다
decoded_newswire = ' '.join([reverse_word_index.get(i - 3, '?') for i in train_data[0]])>>> decoded_newswire
'? ? ? said as a result of its december acquisition of space co it expects earnings per share in 1987 of 1 15 to 1 30 dlrs per share up from 70 cts in 1986 the company said pretax net should rise to nine to 10 mln dlrs from six mln dlrs in 1986 and rental operation revenues to 19 to 22 mln dlrs from 12 5 mln dlrs it said cash flow per share this year should be 2 50 to three dlrs reuter 3'train_data[0]에는 위의 텍스트가 인코딩 되었습니다.
3.5.2 데이터 준비
데이터의 경우 고유의 정수리스트로 존재하기 때문에 데이터를 벡터로 변환합니다.
import numpy as np
def vectorize_sequences(sequences, dimension=10000):
results = np.zeros((len(sequences), dimension))
for i, sequence in enumerate(sequences):
results[i, sequence] = 1.
return results
# 훈련 데이터 벡터 변환
x_train = vectorize_sequences(train_data)
# 테스트 데이터 벡터 변환
x_test = vectorize_sequences(test_data)
# 레이블을 벡터로 변환합니다.
from keras.utils.np_utils import to_categorical
one_hot_train_labels = to_categorical(train_labels)
one_hot_test_labels = to_categorical(test_labels)3.5.3 모델 구성
출력 클래스의 갯수가 2개에서 46개로 늘어났기 때문에, 출력공간의 차원이 훨씬 커졌습니다.
이전에는 Dense층의 은닉층을 16개로 구성했지만 이번 문제의 경우에는 더 늘려야 합니다. 46개의 클래스를 구분하기 위해 16차원의 은닉층만 사용할경우 각 층은 이전층의 출력에서 제공한 정보만 사용할 수 있습니다. 이렇게 규모가 작은 경우에는 첫번째 층부터 만들어온 정보를 완전히 잃게 되는 정보의 병목이 될수 있습니다.
이런 이유로 좀더 규모가 큰 층을 사용하겠습니다 64개의 은닉층을 사용해봅시다.
# 모델 정의하기
model = models.Sequential()
model.add(layers.Dense(64, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(64, activation='relu'))
# 마지막층에 softmax를 사용하여 클래스의 확률 분포를 출력합니다.
model.add(layers.Dense(46, activation='softmax'))
# 모델 컴파일 하기
model.compile(optimizer='rmsprop',
# 다중 분류를 위한 최적화된 손실함수는 categorical_crossentropy입니다.
loss='categorical_crossentropy',
metrics=['accuracy'])softmax 활성화함수
softmax는 입력받은 값을 출력으로 0~1사이의 값으로 모두 정규화하며 출력 값들의 총합은 항상 1이 되는 특성을 가진 함수이다.
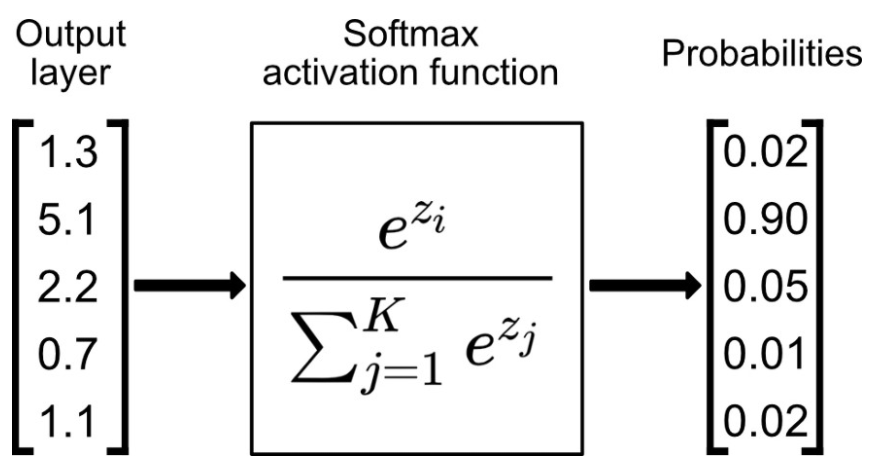
각 입력샘플마다 클래스에 대한 확률 분포를 출력합니다.
3.5.4 훈련검증
해당 모델로 20번의 에포크를 훈련시킬경우, 9번째에서 과대적합이 발생합니다. 그래서 9번의 에포크까지만 훈련을 진행합니다.
# 훈련과 검증데이터로 나눕니다.
x_val = x_train[:1000]
partial_x_train = x_train[1000:]
y_val = one_hot_train_labels[:1000]
partial_y_train = one_hot_train_labels[1000:]
model.fit(partial_x_train,
partial_y_train,
epochs=9,
batch_size=512,
validation_data=(x_val, y_val))
results = model.evaluate(x_test, one_hot_test_labels)3.5.5 새로운 데이터에 대해 예측
최종코드
from keras.datasets import reuters
import numpy as np
from keras.utils.np_utils import to_categorical
from keras import models
from keras import layers
# 로이터 데이터셋 로드하기
(train_data, train_labels), (test_data, test_labels) = reuters.load_data(num_words=10000)
# 벡터변환을위한 함수
def vectorize_sequences(sequences, dimension=10000):
results = np.zeros((len(sequences), dimension))
for i, sequence in enumerate(sequences):
results[i, sequence] = 1.
return results
# 훈련 데이터 벡터 변환
x_train = vectorize_sequences(train_data)
# 테스트 데이터 벡터 변환
x_test = vectorize_sequences(test_data)
# 레이블을 벡터로 변환합니다.
one_hot_train_labels = to_categorical(train_labels)
one_hot_test_labels = to_categorical(test_labels)
# 모델 정의하기
model = models.Sequential()
model.add(layers.Dense(64, activation='relu', input_shape=(10000,)))
model.add(layers.Dense(64, activation='relu'))
# 마지막층에 softmax를 사용하여 클래스의 확률 분포를 출력합니다.
model.add(layers.Dense(46, activation='softmax'))
model.compile(optimizer='rmsprop',
loss='categorical_crossentropy',
metrics=['accuracy'])
# 훈련과 검증데이터로 나눕니다.
x_val = x_train[:1000]
partial_x_train = x_train[1000:]
y_val = one_hot_train_labels[:1000]
partial_y_train = one_hot_train_labels[1000:]
# 모델 훈련시키기
model.fit(partial_x_train,
partial_y_train,
epochs=9,
batch_size=512,
validation_data=(x_val, y_val))
# 결과모델로 테스트데이터 예측하기
results = model.evaluate(x_test, one_hot_test_labels)
print(results)
# predict 메서드는 46개의 토픽에 대한 확률분포를반환한다.
predictions = model.predict(x_test)
print(predictions[0].shape)
print(predictions)결과
>>> results # 78%에 가까운 훈련결과를 갖습니다.
[1.0002825266531505, 0.7867319583892822]
>>> predictions[0].shape # 각항목의 길이는 46
(46,)
>>> predictions # 각항목에 따라 46개의 토픽에대한 확률분포
[[4.91338460e-06 7.92390492e-05 1.52224011e-05 ... 1.55739272e-05
1.60929460e-06 6.42961368e-06]
[6.96766772e-04 3.40056747e-01 3.51194496e-04 ... 8.19293840e-04
5.52320762e-06 1.32637782e-04]
[2.97579623e-04 9.47570860e-01 3.18254833e-03 ... 5.64339163e-04
5.08832200e-05 3.37143691e-04]
...
[1.74893776e-05 3.77911056e-05 1.54958005e-04 ... 1.27051189e-05
1.14225477e-05 1.41094024e-05]
[1.90335629e-03 5.04900627e-02 4.73214546e-03 ... 1.26636354e-03
4.30166285e-04 2.05770973e-03]
[2.29482801e-04 7.69803941e-01 1.34758055e-02 ... 3.03339388e-04
5.53155951e-05 1.92160558e-04]]3.5.6 레이블과 손실을 다루는방법
레이블을 인코딩할때 to_categorical로 변환하는 방법도 있지만, 다음과 같이 정수 텐서로 변환할수도 있습니다.
y_train = np.array(train_labels)
y_test = np.array(test_labels)손실 함수 categorical_crossentropy는 레이블이 범주형 인코딩되어 있을때 사용합니다. 반면 정수 레이블을 사용할 때는 sparse_categorical_crossentropy를 사용해야 합니다.
3.5.7 충분히 큰 중간층을 두어야하는 이유
마지막출력이 46차원이기 때문에 중간층의 은닉층은 46개보다 커야만합니다. 만약 훨씬 작은 중간층 차원이라면 정보의 병목현상이 발생합니다.
model = models.Sequential()
model.add(layers.Dense(64, activation='relu', input_shape=(10000,)))
# 중간의 은닉층은 4개로 해봅시다.
model.add(layers.Dense(4, activation='relu'))
model.add(layers.Dense(46, activation='softmax'))
model.compile(optimizer='rmsprop',
loss='categorical_crossentropy',
metrics=['accuracy'])
model.fit(partial_x_train,
partial_y_train,
epochs=20,
batch_size=128,
validation_data=(x_val, y_val))이럴경우 중간의 정보의병목으로 인해 약 71%의 검증 정확도를 보입니다.
3.6 주택 가격 예측 : 회귀문제
앞의 두 예제는 분류문제입니다. 입력 데이터의 개별적인 레이블(클래스)를 예측하는 것이 목적입니다. 이번에는 개별적인 레이블 대신에 연속적인 값을 예측하는 회귀(regression)입니다. 예를 들어 가상 데이터가 주어졌을 때 내일 기온이나 미래 사건을 예측하는 것입니다.
3.6.1 보스턴 주택 가격 데이터셋
보스턴 주택 가격 데이터셋으로 보스턴 외곽지역의 범죄율, 지방세율에 따라 주택가격의 중간값을 예측해 보겠습니다. 해당 데이터셋은 404개의 훈련샘플과 102개의 테스트 샘프롤 나뉘어 있습니다.
from keras.datasets import boston_housing
(train_data, train_targets), (test_data, test_targets) = boston_housing.load_data()
>>> train_data.shape
(404, 13)
>>> test_data.shape
(102, 13)보다시피 404개의 훈련샘플과 102개의 테스트 샘플이 있고 모두 13개의 수치특성이 있습니다. 13개의 특성들은 1인당 범죄율, 주택당 평균 방의개수, 고속도로 접근성 등입니다.
train_targets과 test_targets에는 주택의 중간가격이 있습니다.
3.6.2 데이터 준비
위 데이터의 경우 너무 편차가 큰 값들이 있습니다. 이럴수록 신경망 학습시 더 어렵게 만든다. 그래서 해당 데이터 특성별 정규화를 진행해야한다.
정규화
정규화란 데이터베이스의 설계를 재구성하는 테크닉입니다. 정규화를 통해 불필요한 데이터(redundancy)를 없앨 수 있고, 삽입/갱신/삭제 시 발생할 수 있는 각종 이상현상(Anamolies)들을 방지할 수 있습니다.
# 특성의 평균을 빼고 표준편차로 나눕니다.
mean = train_data.mean(axis=0)
train_data -= mean
std = train_data.std(axis=0)
train_data /= std
# test 데이터를 정규화할때에도 훈련데이터의 평균과 표준편차를 활용합니다.
test_data -= mean
test_data /= std3.6.3 모델 구성
샘플의 개수가 적기 때문에 64개의 유닛을 가진 은닉층을 활용합니다.
일반적으로 데이터의 개수가 적을수록 과대적합이 더 쉽게 일어나므로 반드시 작은 모델을 활용하여 과대적합을 최소화합시다.
from keras import models
from keras import layers
def build_model():
# 동일한 모델을 여러 번 생성할 것이므로 함수를 만들어 사용합니다
model = models.Sequential()
model.add(layers.Dense(64, activation='relu',
input_shape=(train_data.shape[1],)))
model.add(layers.Dense(64, activation='relu'))
model.add(layers.Dense(1)) # 활성화함수가 존재x
model.compile(optimizer='rmsprop', loss='mse', metrics=['mae'])
return modellayers.Dense(1)
모델의 마지막층을 보면 활성화 함수가 없는것을 확인할수 있습니다. 해당 문제는 연속적인 값을 예측하는 스칼라 회귀문제로서 마지막층은 순수한 선형값이 나오로고 활성화함수룰 제거합니다.
loss = 'msa'
손실함수는 평균제곱오차(mean squared error)를 사용합니다. msa는 예측과 타깃 사이 거리의 제곱입니다. 회귀문제에서 널리 사용되는 손실함수 입니다.
metrics=['mae']
mae는 평균 절대 오차(mean absolute error)로서 예측과 타깃 사이의 거래의 절댓값입니다.
3.6.4 K-겹 검증을 사용한 훈련검증
모델을 평가하기 위해 훈련데이터를 훈련세트와 검증세트로 나눠야합니다. 하지만 해당 데이터셋의 경우 매우 적기 때문에 세트 분류에 따라 정확도의 차이가 발생합니다. 이런 상황에서 K-겹 교차 검증(K-fold cross-validation)을 사용하여 해결할수 있습니다.
아래 그림으로 확인하면 이해하기 쉽습니다.
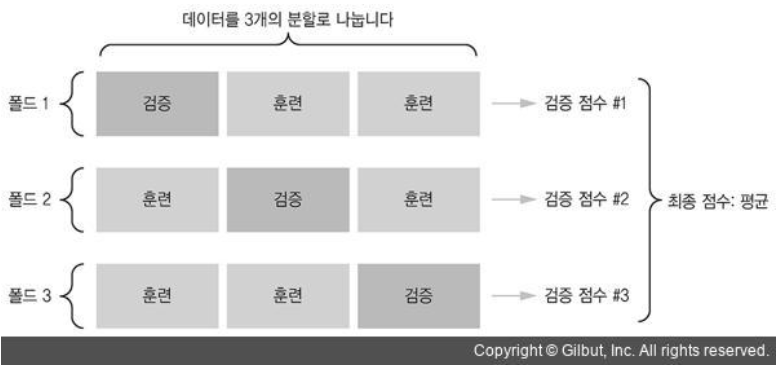
K = 3 일때 하나의 훈련데이터를 K개로 나누고 훈련세트와 검증세트를 번갈아 가면서 훈련과 검증을 K번 진행합니다. 그리고 모델의 검증점수를 구하기 위해 K개의 검증 점수를 평균내면 됩니다.
import numpy as np
k = 4 # 4번의 학습 진행
num_val_samples = len(train_data) // k
num_epochs = 500
all_mae_histories = []
for i in range(k):
print('처리중인 폴드 #', i)
# 검증 데이터 준비: k번째 분할
val_data = train_data[i * num_val_samples: (i + 1) * num_val_samples]
val_targets = train_targets[i * num_val_samples: (i + 1) * num_val_samples]
# 훈련 데이터 준비: 다른 분할 전체
partial_train_data = np.concatenate(
[train_data[:i * num_val_samples],
train_data[(i + 1) * num_val_samples:]],
axis=0)
partial_train_targets = np.concatenate(
[train_targets[:i * num_val_samples],
train_targets[(i + 1) * num_val_samples:]],
axis=0)
# 케라스 모델 구성(컴파일 포함)
model = build_model()
# 모델 훈련(verbose=0 이므로 훈련 과정이 출력되지 않습니다)
history = model.fit(partial_train_data, partial_train_targets,
validation_data=(val_data, val_targets),
epochs=num_epochs, batch_size=1, verbose=0)
# 모든 폴드에 대해 에포크의 MAE점수 평균을 계산합니다.
mae_history = history.history['val_mean_absolute_error']
all_mae_histories.append(mae_history)
# K-겹 검증 점수 평균 기록하기
average_mae_history = [
np.mean([x[i] for x in all_mae_histories]) for i in range(num_epochs)]K-겹 검증 점수의 모든 에포크별 점수를 그래프로 표현해 봅시다.
import matplotlib.pyplot as plt
def smooth_curve(points, factor=0.9):
smoothed_points = []
for point in points:
if smoothed_points:
previous = smoothed_points[-1]
smoothed_points.append(previous * factor + point * (1 - factor))
else:
smoothed_points.append(point)
return smoothed_points
smooth_mae_history = smooth_curve(average_mae_history[10:])
plt.plot(range(1, len(smooth_mae_history) + 1), smooth_mae_history)
plt.xlabel('Epochs')
plt.ylabel('Validation MAE')
plt.show()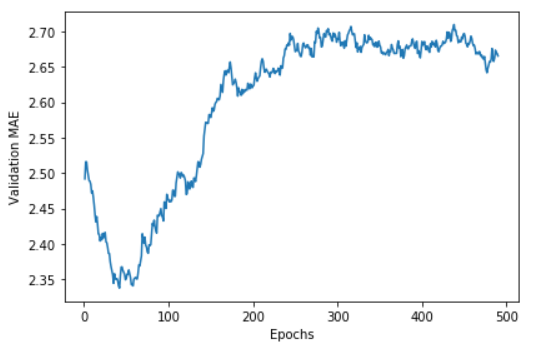
그래프를 확인하면 Validatio MAE은 약 80번의 에포크부터 과대적합이 시작되는걸 볼수있습니다.
최종코드
from keras.datasets import boston_housing
from keras import models
from keras import layers
import numpy as np
(train_data, train_targets), (test_data, test_targets) = boston_housing.load_data()
# 특성의 평균을 빼고 표준편차로 나눕니다.
mean = train_data.mean(axis=0)
train_data -= mean
std = train_data.std(axis=0)
train_data /= std
# test 데이터를 정규화할때에도 훈련데이터의 평균과 표준편차를 활용합니다.
test_data -= mean
test_data /= std
def build_model():
# 동일한 모델을 여러 번 생성할 것이므로 함수를 만들어 사용합니다
model = models.Sequential()
model.add(layers.Dense(64, activation='relu',
input_shape=(train_data.shape[1],)))
model.add(layers.Dense(64, activation='relu'))
model.add(layers.Dense(1)) # 활성화함수가 존재x
model.compile(optimizer='rmsprop', loss='mse', metrics=['mae'])
return model
# 새롭게 컴파인된 모델을 얻습니다
model = build_model()
# 전체 데이터로 훈련시킵니다
model.fit(train_data, train_targets,
epochs=80, batch_size=16)
test_mse_score, test_mae_score = model.evaluate(test_data, test_targets)
>>> test_mse_score, test_mae_score
16.928725448309205 2.686716318130493 테스트를 위한 test_mae_score의 예측 결과 2.686달러 차이나는걸 알수있습니다.
3.6.5 정리
회귀에서 사용하는 손실함수는 MSE !!!!
회귀에서 사용되는 평가지표는 MAE !!!!
데이터가 적다면 K-겹 검증을 사용하는것이 좋습니다 !!!!
데이터가 적다면 과대적합을 피하기 위해 은닉층의 수를 줄인 모델이 좋습니다 !!!!
'Data Science > 딥러닝' 카테고리의 다른 글
| 6장 텍스트 시퀀스를 딥러닝1 (0) | 2020.11.08 |
|---|---|
| 5장 컴퓨터 비전을 위한 딥러닝1 (0) | 2020.10.29 |
| 4장 머신러닝의 기본요소 (0) | 2020.10.28 |
| 5장 컴퓨터 비전을 위한 딥러닝2 (0) | 2020.09.23 |
| 3장 신경망 시작하기1 (0) | 2020.08.31 |
| 2장 시작하기 전에: 신경망의 수학적 구성요소 (0) | 2020.08.31 |